 |
AutoFEM Analysis Forced Oscillation Analysis | ||||||
The goal of Forced Oscillation Analysis
Analysis of forced oscillations is performed to predict the behaviour of a structure under external actions which change in accordance with the harmonic law. These actions include force and/or kinematic excitation. In addition to it, the impact of the system damping may be taken into account.
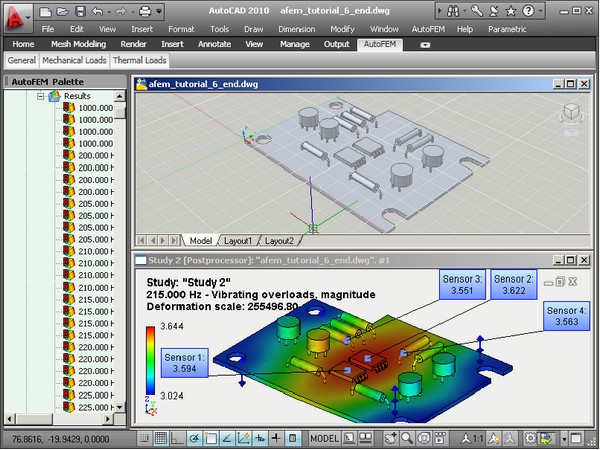
The objective of the forced oscillation analysis is to obtain a dependence of the system’s response on frequency of external vibrations. As a result of calculations we get amplitudes of displacements, vibration acceleration, and vibration overload at the frequency of external source of oscillation. According to these results, one can obtain, for a frequency range, the dependencies of amplitudes and vibration acceleration on frequency of compelling actions, which is important with the evaluation of vibration stability of the system in the preset frequency range.
See also: Forced Oscillation Analysis, Theory Background, Specific Pre-Processor Settings, Steps of Oscillation Analysis, Settings of Oscillation Solver, Analysing Results